Таблица умножения #

В рамках этого проекта мы довольно интересным образом нарисуем таблицу умножения. Для этого придётся вспомнить немного школьной тригонометрии на числовой окружности.

Параметры отрисовки #

Перед тем, как начать рисовать окружность нужно определить некоторые параметры. Так как в программе будет отображаться окружность, то окно программы можно сделать квадратным. Инициализируем окно размера 700 \(\times\) 700 пикселей.

int main()
{
    const int screen_radius = 350;
    const int screen_width = screen_radius * 2;
    const int screen_height = screen_radius * 2;

    InitWindow(screen_width, screen_height, "Creative Coding: Times Table");
    SetTargetFPS(60);
    ...

Для того, чтобы окружность не рисовалась впритык к границе окна, определим переменную радиуса окружности, которая будет чуть меньше радиуса окна. Центр окружности же будет находиться в центре окна.

    ...
    const int radius = screen_radius - 10;
    const Vector2 center = { screen_radius, screen_radius };
    ...

Для того, чтобы нарисовать окружность следует воспользоваться функцией DrawRing. Эта функция принимает следующие аргументы:

void DrawRing(
    Vector2 center,    // Центр окружности
    float innerRadius, // Радиус начала кольца
    float outerRadius, // Радиус окончания кольца
    float startAngle,  // Начальный угол
    float endAngle,    // Конечный угол
    int segments,      // Количество сегментов
    Color color        // Цвет
);

Углы в этой функции передаются в градусах. Так как мы хотим нарисовать полную окружность, то startAngle и endAngle будут соответственно равны 0 и 360.

Радиусы innerRadius и outerRadius укажем равными соответственно radius + 1 и radius + 3, чтобы нарисовать окружность ширины 2.

На самом деле, окружность здесь представляется в виде равностороннего многоугольника, который при достаточном количестве сторон будет неотличим от реальной окружности. Параметр segments отвечает за это количество сторон. Для наших целей будет достаточно 100 сторон.

Добавим в цикл вызов этой функции:

    while (!WindowShouldClose())
    {
        BeginDrawing();
        {
            ClearBackground(BLACK);
            DrawRing(
                center, radius + 1, radius + 3,
                0, 360, 100, WHITE
            );
        }
        EndDrawing();
    }
    CloseWindow();

В результате должна получиться такая картинка:

Теоретическая часть #

Для начала поймём что именно нужно нарисовать.

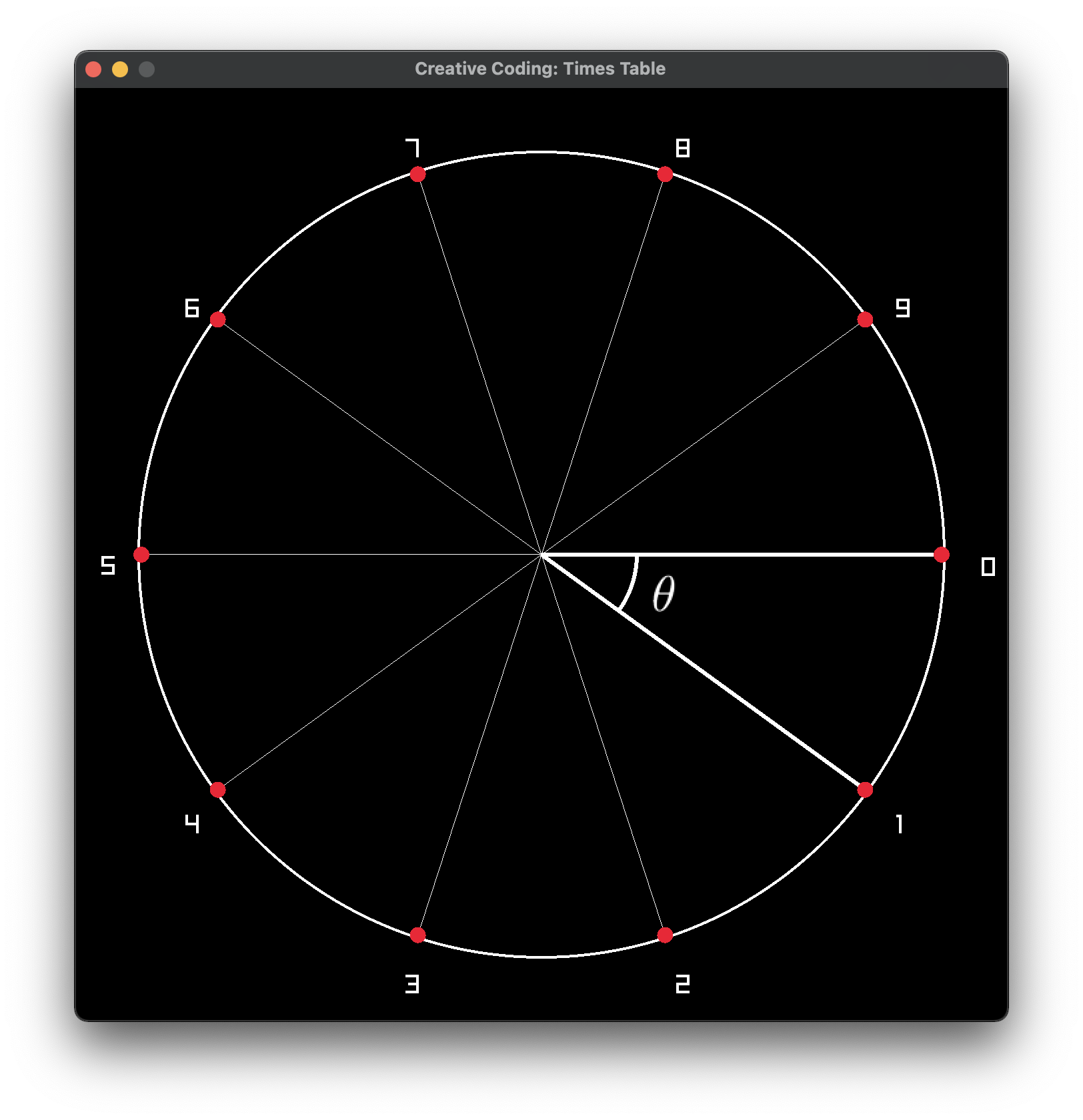
На окружности равномерно отметим некоторое количество точек (например, 10) и пронумеруем их начиная с нуля. Угол между нулевой и первой точками назовём \(\theta\) . Выглядит это примерно так:

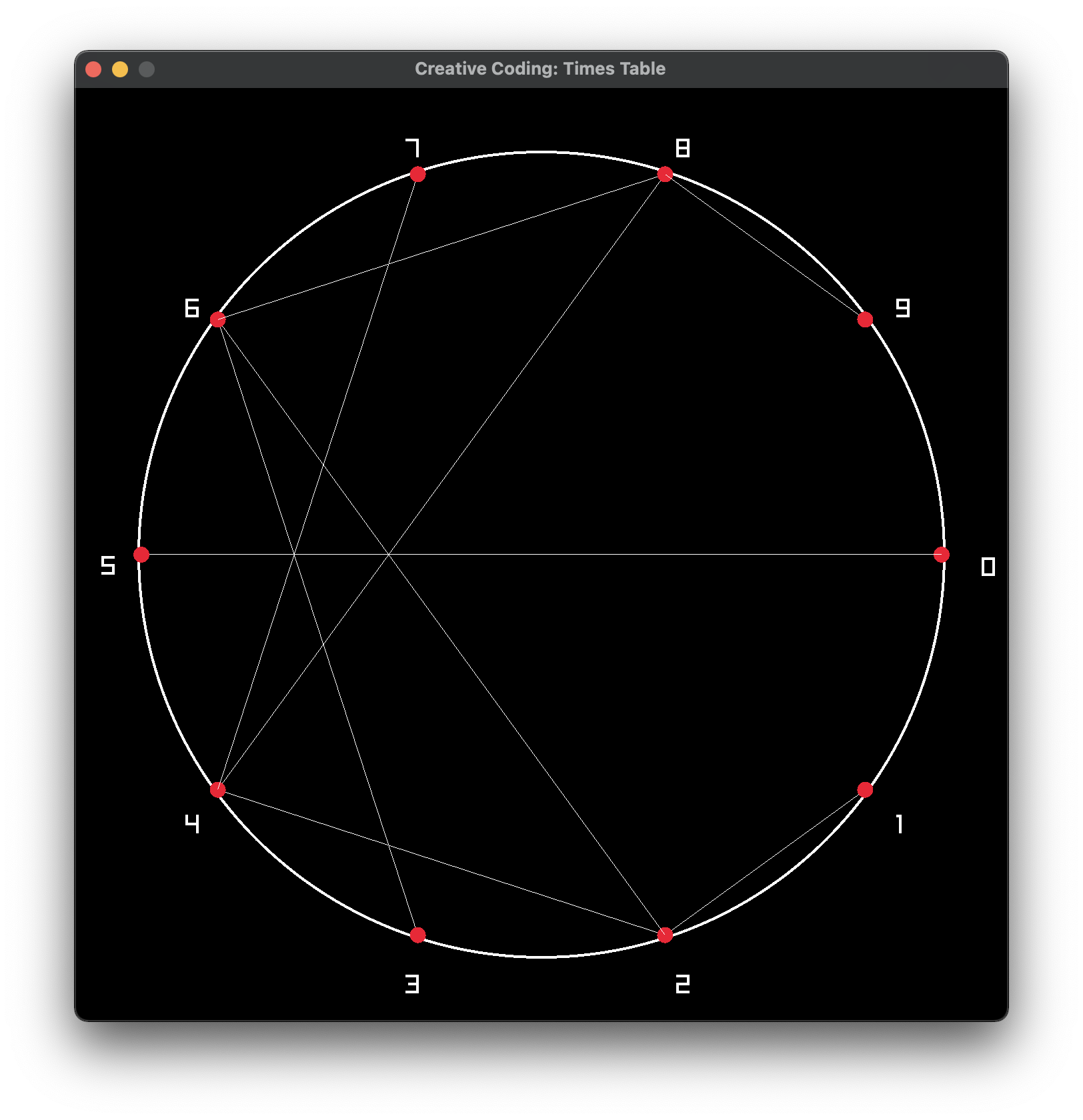
После этого можно соединить каждую точку на окружности, значение которой в \(k\) раз больше (например, на рисунке \(k = 2\) ):

Отрисовка линий #

Добавим в код переменные, отвечающие за количество точек, множитель и угол \(\theta\) . Множитель пока что установим равным 2:

int main() {
    ...
    const int lines_count = 200;
    const float theta = 2.0 * PI / lines_count;

    float multiple = 2.0;
    ...

Внутри основного цикла добавим другой цикл, в котором будут рисоваться все линии:

while (!WindowShouldClose())
{
    BeginDrawing();
    {
        ...
        for (int n = 0; n < lines_count; ++n)
        {
            ...
        }
    }
    EndDrawing();
}

Каждое число на числовой окружности можно преобразовать в координату с помощью такой трансформации:

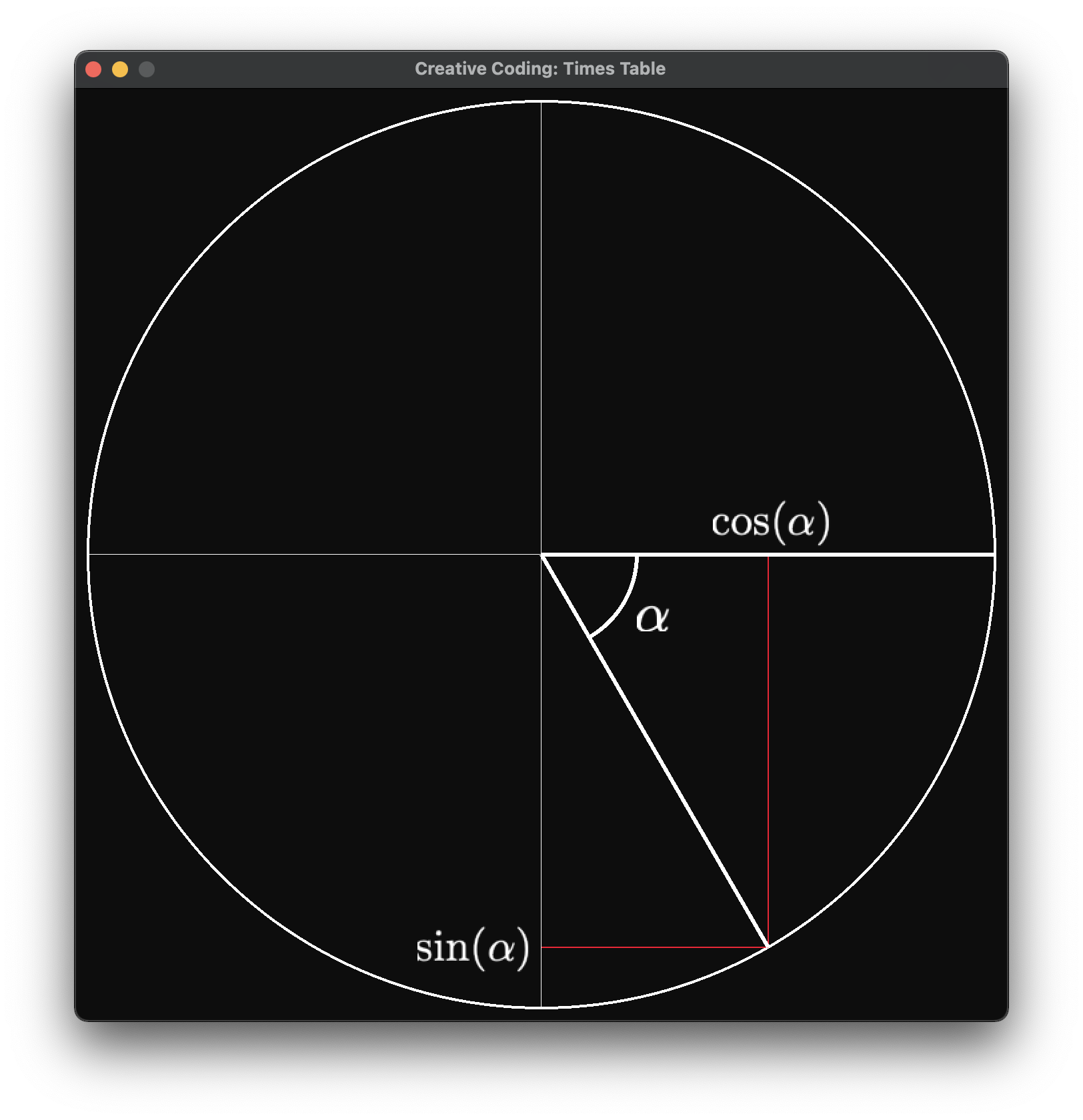
Единице на данной окружности соответствует угол \(\theta\) радиан, поэтому число n умножим на эту константу. Конец же линии находится в некоторой точки, которая в multiple раз больше, чем n. Получаем следующие преобразования:

for (int n = 0; n < lines_count; ++n)
{
    Vector2 start = Vector2 {
        cos(theta * n),
        sin(theta * n)
    } * radius + center;

    Vector2 end = Vector2 {
        cos(theta * multiple * n),
        sin(theta * multiple * n)
    } * radius + center;

    DrawLineV(start, end, WHITE);
}

Попробуем увеличить lines_count с 10 до 200:

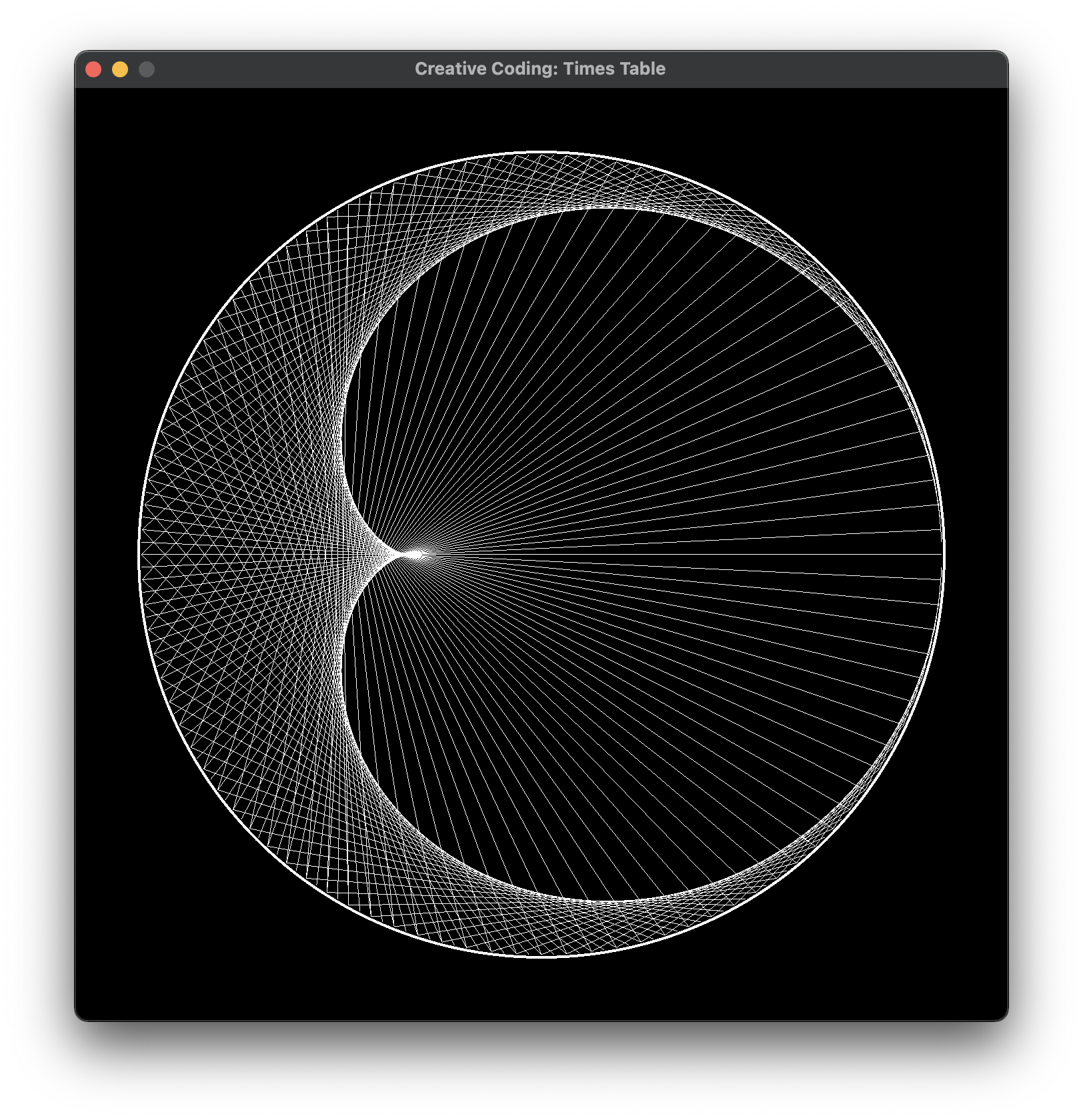
На таком рисунке уже отчётливо видна Кардиоида, которая также встречается в визуализации множества Мандельброта.

Анимация #

Перекомпилировать программу для изменения множителя не очень удобно, поэтому попробуем анимировать изменение параметра. На числовой окружности находятся не только целые числа, поэтому шаг изменения множителя можно сделать действительным числом, чтобы видеть промежуточные рисунки.

Добавим переменную шага и в основном цикле будем прибавлять её к переменной multiple. А саму переменную multiple сделаем равной 1.

int main() {
    ...
    float multiple = 1.0f;
    const float step = 0.01f;
    ...
    while (!WindowShouldClose())
    {
        multiple += step;
    ...

Получим такой рисунок:

Градиент #

В качестве последнего штриха сделаем так, чтобы цвет окружности и линий менялся со временем. Это довольно просто сделать с использованием цветовой модели HSV. В отличие от модели RGB, в HSV оттенок представляется только одной компонентой.

Добавим переменную hue, в которой будет храниться оттенок рисунка, а внутри основного цикла будем создавать цвет с указанным оттенком:

int main() {
    ...
    float hue = 0;
    ...
    while (!WindowShouldClose())
    {
        Color line_color = ColorFromHSV(hue, 1, 1);
        ...

В соответствующих вызовах необходимо поменять передаваемый цвет:

DrawRing(
    center, radius + 1, radius + 3,
    0, 360, 200, line_color
);
...
DrawLineV(start, end, line_color);

После того, как все линии были отрисованы, нужно увеличить значение оттенка на какое-то значение (например, 0.5). Зациклим значение hue, чтобы не происходило никаких ошибок.

while (!WindowShouldClose())
{
    ...
    BeginDrawing();
    {
        ...
        hue += 0.5;
        if (hue > 360) hue = 0;
    }
    EndDrawing();
}

В результате получим такой рисунок:

Готовый код проекта можно посмотреть в нашем репозитории на GitHub.